 |
|
||||||
| منتدى كلية التربية بالجبيل منتدى كلية التربية بالجبيل ; مساحة للتعاون و تبادل الخبرات بين طالبات كلية التربية بالجبيل و نقل آخر الأخبار و المستجدات . |
 |
|
|
أدوات الموضوع |
|
#1
|
||||
|
||||
|
شرح ch1للفيزياء العااااامه
# chapter 1 #
Physics and Measurement يتوقع منك في هذا الفصل أن تعرف: - تقسيم الكميات الفيزيائة " متجهه ، قياسية " - وحدات الكيمات الفيزيائة المشتقه والأساسية ملاحظه : هذا الفصل لا ياتي عليه اسالة مباشره في الأمتحان ولكنه مراجعة ::: 1 ::: الكميات الفيزيائة تصاغ القوانين الفيزيائة عادة بكميات فيزيائة متفق عليها عالمياً مثل " السرعة . التسارع ... الخ " الكمية الفيزيائة هي وسيلة تستخدم لوصف وتمييز ظاهرة فيزيائة تنقسم إلى قسمين : - كميات اساسية : وهي سبع كميات فقط ..! :: الطول Length متر :: الكتلة Mass كيلو غرام :: الزمن Time ثانية :: شدة التيار أمبير :: درجة الحرارة كلفن :: شدة الإضاءة شمعة :: كمية المادة مول :: - كميات مشتقة : من السبع اللي فوق نشتق باقي الكميات الفيزيائة مثلاًُ :: الحجم هو ثلاثة اطوال L × L × L :: ايضاً السرعة هي L/T :: .. الخ //-- ملاحظة : بعض الكميات المستعمل في الفيزياء تسمى كميات تكميله وهي ليست فيزيائة مثل الزاوية .. أو النسبة التقريبة --\\ ::: 2 ::: الوحدات - The units دائماً نسمع أن الكيلو غرام هو معاير قياس كتلة المادة والمتر معيار قياس الطور واحياناً يكون الرطل هو معيار قياس الكتلة والقدم معيار قياس للطول ليش الأختلاف ؟ فيه أكثر من نظام للقياس مثلاً النظام البريطاني يستخدم المعايير الثانية .. والنظام الفرنسي المعايير الأولى .. فصارت مشاكل كثير بسبب الأختلاف ذا عند التحويل وعند إرسال مواصفات ..! الحل .. يكون فيه نظام موحد .. نظام عالمي للوحدات SI أو الـنظام العالمي للوحدات اضغط على الرابط عشان تشوف الكميات الأساسية السبع وفقاً للنظام العالمي SI وبالنسبة للكميات المشتقة نشتقها من الكميات الأسايية .. ولكنها ايضاً موضحة في الجدول http://www.chemie.fu-berlin.de/chemi...ral/si_en.html ::: 3 ::: المعايير - Standards :: وش معنى " كيلو غرام ؟ " ليش ماتكون اي شئ ثاني غير الكليو غرام ؟ بعدين من اللي حدد أن الكيلو غرام هو وزن معين ؟ وحسب أيش حدده ؟ يعني السالفة خبط لزق ؟ طيب أنا بقول أن سيارتي وزنها كيلو غرام  :: ::الكليو غرام .. هو وزن اسطوانة من البلاتين حدد حجم معين للأسطوانه وبعد ماقيس وزنها قرروا أن اي وزن يساوي وزن الأسطوانه يكون كيلو غرام .. الأسطوانه محفوظه في في فرنسا في مكتب الأوزان والمقاييس وصارت هي معيار الوزن .. يمكن لو سرقت الأسطوانه وخربت كل أجهزة الوزن ننسى وش معنى كيلو غرام  //.. نفس الكلام للمتر حدد بانه المسافة اللي يقطها الضوء في الفراغ خلال زمن معين من الثانية .. ايضاً الزمن حدد بالنسبة لعدد أهتزازات اللي تصنعها ذرة عنصر معين ..\\ [/QUOTE] ::: 4 ::: معادلات الأبعاد معادلات الأبعاد رمز يدل على كمية فيزيائة مثلاً الطول L في كل الأحوال سواء كان مقاس بالمتر او الكيلو أو غيره الزمن T في كل الأحوال سواء كان مقاس بالثانية أو الساعة .. الخ الكتلة M .. الكميات المشتقه .. ايضاً يشتق لها معادلات ابعاد مثلاً الحجم عبارة عن ايش ؟ عبارة عن طول × طول × طول V = L * L * L المساحة عبارة عن طول × طول A = L * L لو نبي نعرف الكثافة وهي كمية مشتقه كـ معادلة بعد نقول P = M / V لأن الكثافة عبارة عن كتلة حجم معين مقسوم على مقدار الحجم //.. تستفيد من معادلات الأبعاد مستقبلاًُ في أن لو بغيت توجد وحده معينة لكمية في الكيمياء او الفيزياء او اي شئ .. تقدر توجدها بدون حفظ ..\\ مثال : لو عرفت ان الزمن الدوري T للبندول البسيط يعتمد على طول البندول L وعلى تسارع الجاذبيه الأرضيه .. اشتق القانون الخاص بالزمن الدوري والوحدة الخاصة به ؟ //.. تستفيد من معادلات الأبعاد في التحقق من القوانين الفيزيائية ومدى صحتها ...\\ //.. تستفيد من معادلات الأبعاد في تعيين معادلة بعد لكمية مجهولة البعد ..\\ //.. ايضاً << ياكثر فوائدها بس ماتهمكم يامهندسين .. ايضاً لو بغيت تعين معامل تحول من نظام وحدات إلى نظام آخر تستعمل معادلات الأبعاد ...\\ اليومين الجايه أنزل شرح لـ chapter 3 اللي هو عن الـ vectors " المتجهات لأن د. عمر شرح الـ vectors قبل الـ motion in one dimension " الحركة في بعد واحد " وراح نشمي على مخطط الدكتور ملاحظه : الفصل هذا مقدمة إلى الفيزياء ولا يجي عليه اسئلة في الأمتحان مو كل الي في المنهج راح اشرحه .. ولا كل اللي اشرحه من المنهج بالتوفيق يامهندسين وقريب إن شاء الله شرح المتجهات باسلوب بسيط ومصور ونخلص المنهج كامل في المنتدى إن شاء الله ..//.. الموضوع برعاية فندق المخده عليك والبطانيه علينا ..\\.. منقوووووووووووووووووووووووووووول اتمنى اني فدتكم بشى دعواااتكم وبالتوفيق للجميع .gif)
|
|
|
#2 |
|
أكـاديـمـي
|
رد: شرح ch1للفيزياء العااااامه
chaptrt3 ملاحظة . الـ chapter ذا متقدم على الـ c Vectors ::: 1 ::: ماهي المتجهات ؟ المتجهات طريقة تمثيل رياضية للكميات الفيزيائة . الهدف منها تسهيل مهمة الفيزيائين كيف تسهل المهمة  ؟ ؟افترض أن عندك مبلغ 4 ريال وتبي تقسمه على أثنين من أخوانك يدوياً تعطي الأول ريال .. وتعطي الثاني ريال ثم تعطي الأول ريال آخر وتعطي الثاني ريال آخر وبكذا تكون قسمت الـ 4 ريالات بين اخوانك لكن أفرض لو عندك مبلغ ميلون ريال << ايه هين  .. وتبي تقسمه بين اخوانك بنفس الطريقة السابقة .. شئ متعب! .. ويمكن تجلس ثلاث ايام .. وتبي تقسمه بين اخوانك بنفس الطريقة السابقة .. شئ متعب! .. ويمكن تجلس ثلاث ايام لكن بالرياضيات تقول أن 1000,000 / 2 = 500,000 .. لكل واحد وفي ثانية وحدة تطلع النتيجه يعني التمثيلات الرياضية تسهل المهمة للأعمال اليدوية ماهي اقسام الكيمات الفيزيائة ؟ تنقسم إلى قسمين مثل ماذكر سابقاً كميات قياسية scalar : يكفي لوصفها معرفة العدد والوحدة .. فقط كميات متجهه : عشان تعرفها لازم تعرف اضافة لما سبق " العدد والوحدة " الأتجاه ايضاً أمثله على الكميات المتجهه والكميات الفيزيائة Q ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــ O لو فرضنا عندنا نقطتين Q و O والمسافة بينهم 1 متر .. هنا تكون الكمية اللي هي " المسافة كمية قياسية .. لأن مايهم من وين قسنا المسافة من النقطة Q إلى O اول العكس ولكن المهم .. أنك لو بغيت تنتقل من نقطة إلى اخرى .. لازم تقطع مسافة قدرها 1 متر سواء كان بالأتجاه الأمامي .. او بالعكس المهم هنا هو 1 متر .. وليس 1 متر بأي أتجاه ؟  في هذه الحالة يتغير موضع جسم ما .. من النقطة O وبمسافة 1 متر .. وبإتجاه النقطة Q وهنا تسمى " الأزاحه " والمهم فيها أنتقال الجسم من نقطة إلى اخرى ولكن ضمن أتجاه محدد نسمي المتجه بالطريقة ذي  أما بسهم فوق المتجه أو بخط فوقه أما بسهم فوق المتجه أو بخط فوقه واحياناً يكون بـ Q بخط سميك ولكن لأن الكتابة تكون بقلم ممكن تكون صعبة في هذه الحالة لاحظ أن -  لايمكن عكس إتجاه المتجه أي ان المتجه اللي يمثل الأنتقال من O إلى Q لايمكن عكس إتجاه المتجه أي ان المتجه اللي يمثل الأنتقال من O إلى Q لا يساوي في أي حال من الأحوال المتجه اللي ينتقل من Q بإتجاه O - يمكن القول بأن المتجه QO يساوي المتجه OQ ولكن بإشارة سالبة في القيمة مع الأختلاف في الأتجاه **  المتنجه A يساوي في القيمة المتجه A- ولكن عكسه في الأتجاه ** مما يتكون المتجه ؟  إضافة غلى الراس والذيل .. الأتجاه أو الزاوية ::: 2 ::: نظم الأحداثيات coordinate systems أولاً نظام الأحداثيات المتعامدة perpendicular نظام الأحداثيات المتعامدة يكون بمحور سيني x ومحور صادري y ومحور عيني z متعامدة فيما بينها تتلاقى جميعها في نقطة الأصل (0,0 )  في الصوره تلاحظ أن المتجه V0 يبدا من نقطة الأصل (0, 0) وينتهي في النقطة p0 يسمى النوع هذا متجه الموضع للنقطة p0 إذا متجه الموضع لنقطة ما هو المتجه اللذي يصل بين النقطة وبين نقطة الأصل متجه الأزاحة من النقطة a إلى النقطة b " كما في الصورة " ويساوي حاصل طرح المتجهين بمعنى لو رسمت متجه الموضع للنقطة a ورسم متجه الموضع للنقطة b وطرحت المتجهين من بعض راح تحصل على المنتجه الأزرق الغامق في الرسم أتفقوا الرياضين على أن يكتبون المتنجهات بالصورة هذي (x, y , z ) (5 , 4 , 6 ) 6= x الأول من اليسار 4= y الثاني من اليسار 5= z الثالث من اليسار ثانياً نظام الأحداثيات القطبية polar coordinate هنا تعبر عن المتجه بـ طوله و زاويته فقط .. يعني الطول كمية والزاوية أتجاه  نفترض المتجه A وزاويته  كيف تقدر تستخرج Ax و Ay ؟ بمعلومية القيمة A والزاوية  القانون مشهور جداً ولازم تحفظه عشان تستعمله في تحليل القوى ومشكلة الـ 103 في النقطة ذي اللي هي تحليل القوى  Ax = |A| cos Ax = |A| cos  Ay = = |A| sin Ay = = |A| sin |A| = القمية المطلقة لـلمتجه  = زاوية المتجه ! = زاوية المتجه !وهذا تحليل الالمتجهات إلى مركبتين X و Y تقدر تحفظ القانونين .. لأنهم اساس المادة ؟ لنفرض كان عندك Ax و Ay كيف تجيب الـ |A| والزاوية  ؟ ؟القانون لـ | A |  القانون لـ  tan  = y/x = y/x.../// .. التحويل بين النظامين " المتعامد والقطبي " ... \\\ .. مثال : عبر عن المتجه الواصل بين نقطة الأصل (0 , 0 ) و النقطة ( 3 , 5 ) من خلال نظام الأحداثيات القطبية ؟ الحل : في نظام الأحداثيات المتعامدة أعطى المتجه لــتكون المركبة Ax هي Ax= 5 - 0 = 5 والمركبة Ay= 3-0 = 3 نحدد القيمة من العلاقة  ( 25 + 9 ) = 34 إذا قيمة A تساوي الجذر التربيعي لـ 34 ونحدد الأتجاه من خلال القانون tan  = y/x = y/xحاول تعكس المسالة وتوجد المركبتين X و Y بمعرفة A و  ملاحظه مهمة !! 1- إذا كانت المركبتين Ax و Ay موجبتين اي اكبر من الصفر يكون المتجه A في الربع الأول .. وتكون الزاوية  موجبة وتمثل الزاوية مع المحور السيني الموجب يعني هي نفس الزاوية موجبة وتمثل الزاوية مع المحور السيني الموجب يعني هي نفس الزاوية  2- إذا كانت Ax سالبة و Ay موجبة .. يكون المتجه A في الربع الثاني .. للحصول على الزاوية  مقيسة من المحور السيني يجيب اضافة مقيسة من المحور السيني يجيب اضافة  إلى 180 اي تكون الزاوية هي : إلى 180 اي تكون الزاوية هي : = 180 - ( = 180 - ( ) )3- إذا كانت Ax سالبة , و Ay سالبة ايضاً يكون المتجه A في الربع الثالث وتكون قيمة  مقاسة من المحور السيني الموجب هي مقاسة من المحور السيني الموجب هي  = 180 + ( = 180 + (  ) ) 4- إذا كانت Ax موحبة و Ay سالبة يكون المتجه في الربع الرابع وتكون قيمة  مقاسة من المحور السيني الموجب هي مقاسة من المحور السيني الموجب هي  = 360 - ( = 360 - (  ) )المتجه بنظام متجهات الوحدة unit vectors وش تعريف متجه الوحدة ؟ متجه الوحدة : هو متجه يبلغ طوله المطلق وحدة واحدة ويستخدم لوصف إتجاه أو محور محدد للمحور السيني نستخدم i كـ متجه وحدة وللمحور الصادي نستخدم j كـ متجه وحدة وللمحور اليعني نستخدم K كـ متجه وحدة نفرض عندنا متجه A .. له ثلاث مركبات Ax , Ay , Az .. ! كيف نكتبه بطريقة متجهات الوحدة ؟ A = Axi + Ayj + Azk وش الفائدة من متجهات الوحدة ؟ صفقوني إن لقيتوا فائدة منها للمهندسين .. بس زيادة منهج  مثال: عبر عن المتجه الممثل بنظام الأحداثيات المتعامدةى بمتجه موضع النقطة ( -3 , 5 ) .,. بمتجهات الوحدة ؟ الحل: A = 5 i - 3 j وبس عن كثر الكلام  نتكمل عن الـ properties of the vectors أو عن الخصائص والعمليات المجراه على المتجهات أولاً : تساوي متجهين متى نقول أن المتججه A يساوي المتجه B إذا كان لهما نفس المقدرا ونفس الإتجاه في هذه الحالة نقول أن A = B لكن لو كان لهما نفس المقدار ولكن الأتجاه يختلف هنا نرجع للحالة اللي تكلمنا عنها سابقاً  يعني أن A = - A ثانياً: جمع المتجهات addition of vector لنفرض أن عندك ثلاثة متجهات A و B و C وتبي توصل للمحصله حقتهم ؟ بطريقة الرسم شف الصوره 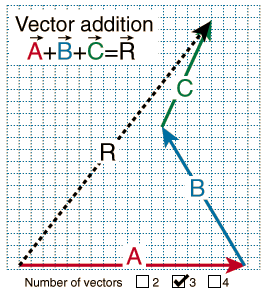 يعني أنك ترسم المتجه A مع أتجاهه وفي نهايته ترسم المتجه B مع الأتجاه وفي النهاية ترسم C مع أتجاهه هنا تحصل على المتجهات الثلاتة مجموعة في محصله أخيره اللي هي R وهي الناتج البياني للجمع //... صور توضح بعض طرق الجمع البياني بطريقة سهله جداً تابع الصور ...\\  سهله مره ! .. لكن كيف تقدر تجمع ذي ؟  مستحيل بالنظر تجيبها .. لأنك ماتعرف الزاوية كم .. وعلى أي أتجاه قيست ؟ يعني الطريقة ذي غير مجديه إلا إذا كان المحور موازي لـ X أو عمودي على الـ Y لكن الرسم البياني دائماً يكون فيه نسبة خطأ اضافة إلى أن الرسم البياني قد لا يكون متوفراً دائماً وإذا توفر ربما لايكون دقيق لذلك تستخدم الرياضيات في جمع المتجهات لإيجاد المحصلة ابي أعطيك خطوات محددة تمشي عليها وبإذن الله أنك ماتخطي في أي عملية جمع متجهات تواجهك في المستقبل لنفرض أن المتجه C أعطي لك بالأحداثيات القطبية وطلب منك جمعه مع المتجه B
بالطريقة ذي تقدر تجمع أي عدد من المتجهات وانت متطمن أن حلك صح تطبيقات الجمع  ثالثاً: طرح المتجهات vector subtraction تكلمنا سابقاً عن طرح متجهين وقلنا : متجه الأزاحة من النقطة a إلى النقطة b " كما في الصورة " ويساوي حاصل طرح المتجهين بمعنى لو رسمت متجه الموضع للنقطة a ورسم متجه الموضع للنقطة b وطرحت المتجهين من بعض راح تحصل على المنتجه الأزرق الغامق في الرسم بياناً لو طلب من طرح متجهين ترسم المتجه الأول لنفرض أنه V ثم ترسم المتجه الثاني W ولكن تعكس أتجاهه يعني كأنك ترسم -W تابع الصوره  مثال حاول أنك تحله ( مهم ) تحركت سيارة 40 كيلو في إتجاه الشمال ، ثم أنعطفت وتحركت 50 كيلو بإتجاه 60 درجه للغرب ، ثم أنعطفت وتحركت 70 كيلو في إتجاه الجنوب . ماهو مقدار وإتجاه المحصله للسيارة ؟ رابعاً: الضرب والمتجهات PRODUCT & VECTORS فيه نوعين من الضرب للمتجهات الأول اسمه الـ SCALAR PRODUCT أو الضرب القياسي وتعريفه هو الكيمة القيساسية الناتجة عن ضرب " مقدار " متجهين في "  cos cos حيث أن  هنا هي الزاوية بين المتجهين هنا هي الزاوية بين المتجهين من الأمثله على هذا الضرب وراح يمر معنا في الدروس القادمه ضرب القوة التي تؤثر على جسم فتزيحه فلو بغينا نحسب الشغل تكون العلاقة  على فرض أن  = t = t لازم تعرف القانون ذا لأن بعدين ينطبق عليه كلام القوى والشغل والأشياء ذي لاحظ هنا تمثل القوى بمتجه ازرق والأزاحة بمتجه اخضر  ومن هنا تجيب القوى والمحصلة  والعلاقة ذي هي ضرب قياسي راح توضح معنا في الدروس القادمة أكثر وأرجع اتكلم عنها مره ثانيه الحين نتكلم عن النوع الثاني اللي هو الضرب المتجه الضرب المتجه نفس الضرب القياسي لكن الفرق بينهم بدل الـ cos نستعمل الـ sin مثلاً المتجه A والمتجه B حاصل الضرب المتجه لهم يكون متجه جديد اسمه C مقداره هو يساوي حاصل ضرب المتجه A في المتجه B في sin الزاوية بينهم  المتجه C يكون عمودياً على A و B في نفس الوقت وله إتجاه معين يحدد بطريقتين الأولى : قاعدة اليد اليمنى تطوي اصابعك الأربع لليد اليمنى في شكل دائرة ويكون الأبهام عمودياً عليها إذا كانت الأصباع الأربع المطويه تشير في إتجاه القوس اللي يبداء من A نحو B يشير الأتجاه للإبهام إلى أتجاه المحور C  الطريقة الثانية طريقة البرغي وهي نفس الطريقة .. لكن بدل أتجاه الأبهام يكون هنا راس البرغي  وبكذا نكون انتهينا من CHAPTAR 3 instantaneous velocity السرعة اللحظية قلنا قبل شوي أن سرعة الجسم ممكن تغير من ( لحظه ) إلى ( لحظه ) خلال حركته في خط مستقيم ولو بغينا أن نوجد سرعة الجسم خلال ( لحظه ) معينة . قبل لا يتغير إلى مستوى ثاني مثلاً لو نقول ان سرعة الجسم عند ( اللحظه ) الفلانيه هي S هذا يعني أن سرعة الجسم عندما يقتر الوقت من ( اللحظه الفلانيه ) هو S ولكن يمكن في لحظه بعدها تكون السرعة مختلفه العلاقية بينهم نفس العلاقة السابقة ولكن نوجد السرعة عندما يقترب الزمن من لحظه معينة من خلال التفاضل ::: 3 ::: معادلات الحركة في خط مستقيم kinematic equation in one dimension: هنا الخلاصة .. ! هناك ثلاث معادلات رئيسة تعرف بالميكانيكا باسم معادلات الحركة inematic equation وتشتق المعادلة الأولى مباشرة من تعريف التسارع ، نفرض أن جسما ما يتحرك بسرعة ابتدائية v0 ، وبتسارع a ، بحيث أصبحت سرعته النهائية v وبعد مرور فترة زمنية مقدارها t ثانية ، بذلك فإنه وفقا لتعريف التسارع a فإنه يكون :  حيث رمزنا للفترة الزمنية التي تسارع خلالها الجسم بالرمز t بدلا من ∆t ويمكن كتابة العلاقة في الصورة التالية : v = v0 + a t وتعرف باسم المعادلة الأولى للحركة .. وللاشتقاق المعادلة الثانية للحركة ينبغي استرجاع تعريف الإزاحة بدلالة السرعة المتوسطة vav فإذا كان x1=0 و عبرنا عن الفترة الزمنيه بالرمز t بدلا من ∆t تكون الإزاحة x بدلا من x2 - x1 هي : x = vav t وحيث أن سرعة الجسم تتغير بمرو الزمن بسبب تحركه بتسارع منتظمa فإنه يمكن حساب السرعة المتوسطة بيسر كمتوسط حسابي للسرعة الابتدائية v0 والسرعة النهائية v أي أن : vav = ( v0 + v ) / 2 وبالتعويض عن قيمة في المعادلة الأولى للحركة واستبدال vav في العلاقة السابقة بقيمتها الجديدة ، فإن : x = v0 t + ( ½ ) a t2 وتعرف هذه المعادلة بالمعادلة الثانية للحركة . وتجدر الإشارة إلى أنه إذا لم تكن إحداثيات الجسم عند اللحظة الابتدائية t1 مساوية للصفر ( أي إذا لم تكن x1 = 0 ) فإنه ينبغي جمع الإزاحة في لحظة الصفر x0 إلى الإزاحة المحسوبة بالعلاقة: x = v0 t + ( ½ ) a t2 أي أنه : x = x0 + v0 t + ( ½ ) a t2 أما المعادلة الثالثة للحركة فتشتق من كل من المعادلة الأولى والثانية بعد التخلص من الزمن في هاتين المعادلتين ، يكون الزمن  وبالتعويض عن الزمن t في المعادلة: x = v0 t + ( ½ ) a t2 وبعد إعادة الترتيب فإنها تتخذ الصورة : v2 = v02 + 2 a x وهذه هي معادلة الحركة الثالثة . وعندما تكون الازاحة الابتدائية x0 ≠ 0 فإنه تتخذ المعادلة v2 = v02 + 2 a x الصورة : v2 = v02 + 2 a ( x – x0 ) ..// الخلاصة \\.. ويلاحظ أن أي معادلة من معادلات الحركة الثالثة تتضمن أربعة متغيرات من بين المتغيرات الخمسة للحركة .. فالمعادلة الأولى لا تتضمن الإزاحة .. والمعادلة الثانية لا تضمن السرعة النهائية للجسم والمعادلة الثالثة لا تتضمن الزمن وبالتالي تتمثل أي مسألة من مسائل الحركة في معرفة ثلاثة عناصر ( ثلاثة متغيرات ) ومعرفة المطلوب الرابع ( أي المتغير الرابع ) واختيار المعادلة التي تتضمن هذه المتغيرات الأربعة وتطبيقها لاستنباط المطلوب. يعني بالعربي أنت عندك ثلاث معادلات وخمس متغيرات وكل معادله تتضمن مجهول متغير شغل رياضيات ...! وتكون ماشي في الحل السليم تلميحات : - إذا كان الجسم يبداء من السكون فإن ( سرعته الأبتدائية = صفر ) - إذا كان الجسم يبداء من X1 وينتهي في X2 يكون التغير في المسافة هو X2 - X1 - نفس الملاحظه في الأعلى للـ T اللي هو الزمن - التسارع دائماً ثابت ! ::: 4 ::: السقوط الحر ..! يقصد بالسقوط الحر للجسم : تحرك هذا الجسم بحرية تحت تأثير الجاذبية الأرضية دون النظر لحالته الحركية الابتدائية .. فالجسم الذي يُـقذف رأسيا لأعلى أو لأسفل ، أو ذلك الذي يسقط سقوطا حرا من موضعه الابتدائي ، تعتبر جميعها خاضعة للسقوط الحر طالما لا تخضع هذه الأجسام لقوى أخرى سوى الجاذبية . ومن البديهي أن هذا الجسم سيخضع دائما لتسارع الجاذبية الأرضية g = 9.8 m /sec2 ) ) الذي يؤدي إلى جذب الأجسام دائما لأسفل وعند إهمال القوة الناتجة عن احتكاك الجسم بالهواء ، واعتبار أن تسارع الجاذبية لا يتغير بتغير الارتفاع عن سطح البحر ، فإنه يمكن اعتبار حركة السقوط الحر للجسم مكافئة تماما لحركته في اتجاه واحد تحت تأثير تسارع ثابت ، وبالتالي يمكن تطبيق نفس معادلات الحركة على الجسم الساقط سقوطا حرا مع استبدال المحور الأفقي x بمحور الحركة الرأسي ( المحور الصادي y ) تنبيه .. حتى تتخلص من الأخطاء الناجمة عن الاختيار غير الصحيح للاتجاهات والتي تؤدي إلى حدوث التباس في إشارات حدود المعاملات ، لذا ينبغي الالتزام بالقواعد الأساسية المعمول بها ، والتي تتلخص في الآتي : 1- أية إزاحة لأعلى تعتبر موجبة ( + y ) ، وأية إزاحة لأسفل تعتبر سالبة (- y ) لإيضاح ذلك : مثلا .. إذا تحرك جسم من نقطة بداية الحركة لأعلى 40 م يقال أنه حدثت له إزاحة y = 40 m وإذا تحرك لأسفل 20 م من نقطة البداية يقال أن الإزاحة y = - 20 وإذا تحرك جسم من نقطة البداية لأعلى 40 م ثم هبط بعد ذلك 30 م تكون إزاحته : y = 40 - 30 = 10 m أما إذا تحرك لأعلى 40 م ،ثم هبط لأسفل 50 م تكون إزاحته الصافية : y = 40 - 50 = - 10 m 2- إذا كان الجسم متحركا لأعلى ( أي اتجاه لأعلى دون النظر لموضع الجسم بالنسبة لنقطة بداية الحركة ) عند نقطة ما ، فمعنى ذلك أن سرعته سواء الابتدائية أو النهاية عند هذه النقطة موجبة ، أما إذا كان اتجاه حركة الجسم لأسفل فمعنى ذلك أن سرعته سواء الابتدائية أو النهاية عند هذه النقطة سالبة. 3- حيث أن تسارع الجاذبية الأرضية يتجه – دائما – رأسيا لأسفل فإنه يكون دائما بالسالب ، أي أنه يجب استبدال a في معادلات الحركة بتسارع الجاذبية g وبإتباع هذه القواعد تتخذ معادلات الحركة للسقوط الحر الصور التالية : v = v0 – g t ( 1 ) y = v0 t – ½ g t2 ( 2 ) v2 = v02 - 2 g y ( 3 ) وعندما لا تنطبق نقطة بداية الحركة مع نقطة أصل المحور الرأسي ، أي عندما تكون هناك إزاحة ابتدائية y0 ، تبد الحركة منها تتخذ العلاقتان ( 3 ) و( ( 2 الصورة التالية : y = y0 + v0 t – 1 g t2 v2 = v02 - 2 g ( y – y0 ) 4 – عندما يصل الجسم المقذوف لأعلى نقطة ( أقصى ارتفاع له ) تكون سرعته عند هذه النقطة مساويا للصفر ، ويبدأ في الهبوط لأسفل ، أي يتغير اتجاه السرعة من الموجب إلى السالب بمجرد تغيير الجسم لاتجاه حركته . ملخص لكل الكلام اللي فوق .. وللناس اللي تحب تفحظ ! معادلات الحركة في خط مستقيم kinematic equation in one dimension : هناك ثلاث معادلات رئيسة تعرف بالميكانيكا باسم معادلات الحركة inematic equation المعادلة الأولى : v = v0 + a t المعادلة الثانية : x = v0 t + ( ½ ) a t2 المعادلة الثالثة : v2 = v02 + 2 a x احفظ الثلاث معادلات واتبع الخطوات ذي - طلع المتغيرات المعلومة على جنب - شف اي معادله من الثلاث يجمعهم - عوض عن قيمتهم واحصل على مجهولك - إذا كان في المسالة ربط حركتين ..( عامل كل حركة على انها مستقله في البداية وبعدين أوجد الرابط وغالباً يكون الزمن أو نقطة النهائية ) وكمل حلك -- السقوط الحر للأجسام Free falling of bodies : يعرف بأنه: تحرك الجسم بحرية تحت تأثير الجاذبية الأرضية(g = 9.8 ) دون النظر لحالته الحركية الابتدائية . تتخذ معادلات الحركة للسقوط الحر الصور التالية : المعادلة الأولى v = v0 – g t المعادلة الثانية y = v0 t – ½ g t2 المعادلة الثالثة v2 = v02 - 2 g y احفظ الثلاث معادلات واتبع الخطوات ذي - طلع المتغيرات المعلومة على جنب - شف اي معادله من الثلاث يجمعهم - عوض عن قيمتهم واحصل على مجهولك - إذا كان في المسالة ربط حركتين ..( عامل كل حركة على انها مستقله في البداية وبعدين أوجد الرابط وغالباً يكون الزمن أو نقطة النهائية ) وكمل حلك وبث  |

|
|
|
#3 | |
|
أكـاديـمـي فـعّـال
|
رد: شرح ch1للفيزياء العااااامه
اقتباس:
.gif) .gif) الموضوع روعة فهمت اشياء منه وطريقة الشرح واضحة تسلمييين ي قمر  
|
|

|
|
|
#4 |
|
أكـاديـمـي
|
رد: شرح ch1للفيزياء العااااامه
يسسلمو ما قصصرتي الله يسسهل آمورك
 
|

|
|
|
#5 |
|
أكـاديـمـي ذهـبـي
|
رد: شرح ch1للفيزياء العااااامه
مآ قصرتي ربي يوفقكّ
 الشرح جداً مُبسط ووآضح .gif)
|

|
|
|
#6 |
|
أكـاديـمـي
|
رد: شرح ch1للفيزياء العااااامه
( جدول ( 1 مفردات المقرر في التعليم الجامعي مفردات المقرر في التعليم العام SYLLABUS الفصل الول : الفيزياء و القياس. معايير الطول والكتلة والزمن, تحليل البعاد ,حفظ الوحدات. الفصل 1 Serway في كتاب الصفحة من 2 إلى 12 Chapter 1 : Physics and . Measurement Standards of Length Mass and Time , Dimensional Analysis , Conservation of Units : Serway Ch. 1: Page2-12 ( - الفيزياء والقياس: (الول الثانوي ص 12 - المفاهيم الساسية: ]الطول , الكتلة , الزمن[ , ]المسافة , الحجم , السرعة[ ( (الول الثانوي ص 15 - الوحدات و المقاييس: الطول ]المتر[, الكتلة ]كيلو جرام[, الزمن ]الثانية[ ( (الول الثانوي ص 14 .( - تحليل البعاد: "اشتقاق القوانين" (الول الثانوي ص 16 - حفظ الوحدات: ل يوجد في التعليم العام. الفصل الثاني : الحركة في اتجاه واحد. الزاحة, السرعة, السرعة اللحظية, التسارع, الحركة الخطية المنتظمة, السقوط الحر. الفصل 2 Serway في كتاب الصفحة من 24 إلى 40 Chapter 2 : Motion in One . Dimension Position , Velocity , , Instantaneous Velocity Acceleration ,One Dimension Motion with Constant Acceleration, Freely Falling .Objects : Serway Ch. 2 : Page24-40 ( - الحركة في اتجاه واحد : (الول الثانوي ص 22 س = س 2 – س 1 , حيث: Δ : - الزاحة س 1: المسافة البتدائية. ,س 2: المسافة النهائية. ( (الول الثانوي ص 23 والثاني المتوسط الفصل الول ص 102 - السرعة : ع = ف \ ز ,حيث:ف :المسافة. , ز :الزمن. (الول الثانوي ص 23 والثاني الثانوي الفصل الول ص 125 والثاني المتوسط الفصل ( الول ص 104 ( - السرعة اللحظية : وتكون عند لحظة زمنية معينة. (الول الثانوي ص 24 ز ,حيث: Δ \ عΔ = - التسارع : ت ز :الفرق في الزمن. Δ , . ع :الفرق في السرعة Δ ( (الول الثانوي ص 26 والثاني الثانوي الفصل الول ص 94 - الحركة الخطية المنتظمة : 1- ع 1 = ع 0 + ت ز 2 ت ز 2 \1 + -2 ف = ع 0 -3 ع 1 2 = ع 0 2 ت ف + 2 ( (الثاني الثانوي الفصل الول ص 128 - السقوط الحر : بسبب تسارع الجاذبية الرضية . حيث تسارع الجاذبية الرضية هي : ج = 8,9 م \ ث 2 ( (الول الثانوي ص 29 29( جدول ( 2 مفردات المقرر في التعليم الجامعي مفردات المقرر في التعليم العام SYLLABUS الفصل الثالث : المتجهات. محاور السناد المرجعية, تحليل المتجهات, مركبة المتجه, متجهات الوحدة, خصائص المتجهات, ضرب المتجهات. الفصل 3 Serway في كتاب الصفحة من 59 إلى 65 .Chapter 3 : Vectors Coordinate Systems , Vector and scalar Quantities, Components of Vector , Unit Vectors , Some Properties of , Vectors . Multiplying a Vector : Serway Ch. 3 : Page59-65 ( - إطار السناد : (الول الثانوي ص 22 والثاني المتوسط الفصل الول ص 95 ( - تحليل القوى : (الثاني الثانوي الفصل الول ص 39 ( - مركبة المتجه : (الثاني الثانوي الفصل الول ص 41 ( - خصائص المتجهات : 1- نقل المتجهات (الثاني الثانوي الفصل الول ص 13 ( -2 جمع المتجهات (الثاني الثانوي الفصل الول ص 15 ( 3 - ضرب المتجهات (الثاني الثانوي الفصل الول ص 19 0 م 2 = م 1 م 2 جتاه ,حيث: - ضرب المتجهات : 1- ضرب قياسي ( 0) م 1 م 1:متجه 1 ,م 2:متجه 2 ,ه:الزاويه بينهما , (الثاني الثانوي الفصل الول ص (19 م 2 = م 1 م 2 جاه = م 3 ,حيث: x م 1 (X) -2 ضرب متجه م 3 : متجه جديد (الثاني الثانوي الفصل الول ص (20 الفصل الرابع : الحركة في اتجاهين. الزاحة, السرعة, التسارع, الحركة في بعدين, المقذوفات, الحركة الدائرية. الفصل 4 Serway في كتاب الصفحة من 78 إلى 91 Chapter 4 : Motion in Two .Dimension Position , Velocity , Acceleration ,Tow Dimension Motion with Constant Acceleration , Projectile Motion , Uniform Circular .Motion In Serway Book is Ch. 4 : Page 78-91 ( - الزاحة : (الول الثانوي ص 23 و الثاني المتوسط الفصل الول ص 102 - السرعة :(الول الثانوي ص 23 و الثاني الثانوي الفصل الول ص 125 والثاني ( المتوسط الفصل الول ص 104 ( - التسارع : (الول الثانوي ص 26 و الثاني الثانوي الفصل الول ص 94 ( - الحركة في بعدين: (الثاني الثانوي الفصل الول ص 128 - المقذوفات: 1- المقذوفات الرأسية ]السقوط الحر[ -2 المقذوفات الفقية ]قذائف المدافع[ ( (الثاني الثانوي الفصل الول ص 135 - الحركة الدائرية: ( (الثاني الثانوي الفصل الول ص 147 و الثاني المتوسط الفصل الول ص 108 30 جدول( 3 مفردات المقرر في التعليم الجامعي مفردات المقرر في التعليم العام SYLLABUS الفصل الخامس: قوانين نيوتن للحركة. مفهوم القوة, قانون نيوتن الول للحركة, الكتلة, قانون نيوتن الثاني للحركة, قوة الجاذبية, الوزن, قانون نيوتن الثالث للحركة, تطبيقات على قوانين نيوتن, قوى الحتكاك. الفصل 5 Serway في كتاب الصفحة من 112 إلى 131 Chapter 5 : The Laws of .Motion , The Concept of Force Newton 1`st Law , Mass , Newton 2`nd Law , The Gravitational Force , Weight , Newton 3`rd Law , Some Applications of Newton`s Laws , Forces of .Friction : Serway Ch. 5 : Page112-131 ( - مفهوم القوة : (الول الثانوي ص 36 - قانون نيوتن الول : مجموع القوى = صفر ( (الول الثانوي ص 36 و الثاني الثانوي الفصل الول ص 93 ت ,حيث: ك: الكتلة. , ت: التسارع. x - قانون نيوتن الثاني : ق = ك ( (الول الثانوي ص 38 و الثاني الثانوي الفصل الول ص 98 - قانون الجذب العام : ق = ج ك 1 ك 2 \ ف 2 , حيث : ك 1,ك 2: كتلتا الجسمين. x 10-11 ف: المسافة بين مركزي الجسمين. ج: ثابت الجذب العام = 7,6 ( (الول الثانوي ص 42 و الثاني الثانوي الفصل الول ص 117 ج , حيث: x - الوزن : ق = ك ( ك: كتلة الجسم. ج: الجاذبية الرضية = 8,9 م \ ث 2 (الول الثانوي ص 40 - قانون نيوتن الثالث : ق أب = ق ب أ ,حيث : ق أب : القوة من الجسم أ إلى ( الجسم ب (الول الثانوي ص 42 و الثاني الثانوي الفصل الول ص 104 ( - تطبيقات على قوانين نيوتن : (الول الثانوي ص 43 ( - الحتكاك : (الثاني الثانوي الفصل الول ص 110 والول الثانوي ص 44 جدول ( 4 مفردات المقرر في التعليم الجامعي مفردات المقرر في التعليم العام SYLLABUS الفصل السابع والثامن: الطاقة ونقل الطاقة. الشغل الناتج عن قوة ثابتة, الشغل الناتج عن قوة متغيرة, الطاقة الحركية, قانون حفظ الطاقة, القدرة, الطاقة الكامنة, القوى المحافظة وغير المحافظة, العلقة بين القوى المحافظة والطاقة الكامنة, التغير في الطاقة الميكانيكية للقوى المحافظة, قانون حفظ الطاقة الميكانيكية لنظام معزول, الحالة التي تتضمن ا حركيا, نظرية الشغل . احتكاك والطاقة. الفصل 7 و 8 Serway في كتاب الصفحة من 183 إلى 234 Chapter 7 & 8 : Energy and .Energy Transfer Work Done by Constant Force ,Work Done by Varying Force ,Kinetic Energy ,The Nonisolated System-Conservation of Energy, Power , Potential Energy, Conservation and Nonconservation Forces , Relationship Between Conservation Forces and Potential Energy , Changes in Mechanical Energy For Non conservation Forces , The Isolated System- Conservation of Mechanical Energy , Situation Involving Kinetic Friction , The Work- .Kinetic Energy Theorem : Serway Ch. 7 & 8 : Page183-234 - حساب الشغل لقوة ثابتة : شغ = ق 0 ف 0 جتاه ,حيث : ق:القوة المؤثرة على جسم. ف: الزاحة الناتجة عن القوة. ه: الزاوية بين القوة والجسم. ( (الثاني الثانوي الفصل الثاني ص 9 - حساب الشغل لقوة متغيرة : شغ = المساحة تحت المنحنى ( (الثاني الثانوي الفصل الثاني ص 11 2 ك ع 2 \ - الطاقة الحركية: طح = 1 (الثالث المتوسط الفصل الثاني ص 51 و الول الثانوي ص 54 و الثاني الثانوي الفصل ( الثاني ص 18 - قانون حفظ الطاقة: (الثالث المتوسط الفصل الثاني ص 58 و الول الثانوي ص 56 و الثاني الثانوي الفصل ( الثاني ص 30 - القدرة: قد = شغ \ ز ,حيث: ز: الزمن المستغرق ( (الثاني الثانوي الفصل الثاني ص 15 - الطاقة الكامنة: طك = ج ك ف ,حيث: ج: الجاذبية الرضية = 8,9 م \ ث 2 ك: كتلة الجسم. ف: ارتفاع الجسم عن سطح الرض. (الثالث المتوسط الفصل الثاني ص 54 و الول الثانوي ص 54 و الثاني الثانوي الفصل ( الثاني ص 19 - التغير في الطاقة الميكانيكية للقوى المحافظة: ( (الثاني الثانوي الفصل الثاني ص 26 - قانون حفظ الطاقة الميكانيكية لنظام معزول : مجموع شغ = صفر ( (الثاني الثانوي الفصل الثاني ص 29 ق ع ,حيث: ق أ : قوة الحتكاك x : ق أ = أ . - الحالة التي تتضمن احتكاكا الحركي . أ: ثابت الحتكاك. , ق ع : قوة رد الفعل العمودي من السطح على الجسم. (الثالث المتوسط الفصل الثاني ص 60 و الول الثانوي ص 44 و الثاني الثانوي الفصل ( الول ص 110 طك Δ + طح Δ = - نظرية الشغل والطاقة: مجموع شغ (الثالث المتوسط الفصل الثاني ص 47 و الول الثانوي ص 53 و الثاني الثانوي الفصل ( الثاني ص 1 |

|
|
|
#7 |
|
أكـاديـمـي نــشـط
|
رد: شرح ch1للفيزياء العااااامه
كلي فدآآ ..
مره مره مره شكككككرن  شرحك جميل وبسيط .. كنت محتاجته 
|

|
|
|
#8 |
|
أكـاديـمـي فـعّـال
|
رد: شرح ch1للفيزياء العااااامه
يعطيك العافيه
ربي يوفقكككك ياعسسل 
|

|
|
|
#9 |
|
أكـاديـمـي نــشـط
|
رد: شرح ch1للفيزياء العااااامه
مشكوووووووررررررررره ان شششششششششششاء الله فل مارك
>> ميرسسي النوري 
|

|
|
|
#10 |
|
أكـاديـمـي نــشـط
|
رد: شرح ch1للفيزياء العااااامه
^
وحده بمخي النوري ** .gif)
|

|
 |
| مواقع النشر (المفضلة) |
| الذين يشاهدون محتوى الموضوع الآن : 1 ( الأعضاء 0 والزوار 1) | |
|
|