السلام عليكم ورحمة الله

هذه المحاضرة تعتمد على :

http://www.ckfu.org/vb/t515925.html
http://www.ckfu.org/vb/t514278.html

تطرقنا في المحاضرة العاشرة إلى اشتقاق الدوال ، و في هذه المحاضرة سنتطرق إلى بعض الدوال الخاصة و هي الدالة الأسية و اللوغاريتمية و المثلثية وهي الدوال التي عرجنا عليهن في المحاضرة السادسة .


أ ) مشتقة الدالة الأسية

ولها 3 حالات :

1 / إذا كان الأساس هو العدد النيبيري e و الأس هو x
فإن المشتقة التفاضلية لهذه الدالة الأسية مساوية لنفسها




2 / إذا كان الأساس هو العدد النيبيري e و كان الأس كثير الحدود
فإن المشتقة التفاضلية تتكون من جزئين :

الدالة الأصلية * تفاضل الأس





3 / إذا كان الأساس هو a حيث أن a هو عدد حقيقي معلوم ، و كان الأس كثير الحدود x
فإن المشتقة التفاضلية تتكون من جزئين :

الدالة الأصلية * لوغاريتم الأساس





ب) مشتقة الدالة الوغاريتمية .


ولها حالتان :

1/ إذا كان اللوغاريتم طبيعي ln

فتكون المشتقة الأولى للدالة هي = مشتقة الدالة ÷ الدالة الأصلية





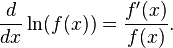2/ إذا كان اللوغاريتم عادي log

فتكون المشتقة الأولى للدالة هي = 1 ÷ (x ln b)



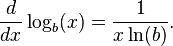
حيث أن x هو العدد و أن b هو أساس اللوغاريتم



ج) مشتقة الدالة المثلثية .



لقيتها من فاعل خير